分类讨论思想是一种重要的数学思想方法，当问题的对象不能进行统一研究时，就需要对研究的对象按某个标准进行分类，然后对每一类分别研究，给出每一类的结论，最终综合各类结果得到整个问题的解答．实质上分类讨论就是“化整为零，各个击破，再集零为整”的数学策略．

引起分类讨论的原因主要是以下几个方面：

1．由取值范围引起的分类讨论。

2．由图形的运动（位置不确定）引起的分类讨论。例如，等腰三角形一腰上的高与另一腰所成的夹角为45°，求顶角的度数．首先根据题意画出图形，一种情况等腰三角形为锐角三角形，即可推出顶角的度数为45°．另一种情况等腰三角形为钝角三角形，由题意，即可推出顶角的度数为135°．

分类讨论的基本步骤：

（1）确定讨论的对象和讨论的范围；

（2）确定分类的标准，进行合理的分类，分类要“既不重复，也不遗漏”；

（3）对多级讨论，应逐级进行，不能越级；

（4）总结概括，得出结论．

【典型例题】

（14广东）如图，在△ABC中，AB＝AC，AD⊥BC于点D，BC＝10cm，AD＝8cm．点P从点B出发，在线段BC上以每秒3cm的速度向点C匀速运动，与此同时，垂直于AD的直线m从底边BC出发，以每秒2cm的速度沿DA方向匀速平移，分别交AB、AC、AD于E、F、H，当点P到达点C时，点P与直线m同时停止运动，设运动时间为t秒（t＞0）．

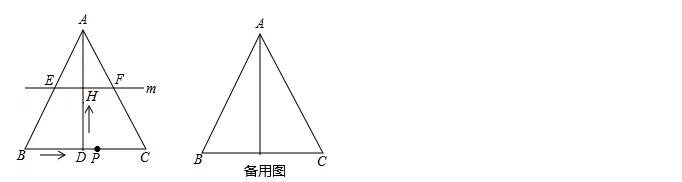
（1）当t＝2时，连接DE、DF，求证：四边形AEDF为菱形；

（2）在整个运动过程中，所形成的△PEF的面积存在最大值，当△PEF的面积最大时，求线段BP的长；

（3）是否存在某一时刻t，使△PEF为直角三角形？若存在，请求出此时刻t的值；若不存在，请说明理由．