一、试卷结构分析

试题分值：150        及格分数： 90

考试范围：解三角形、数列、立体几何、直线与圆、椭圆

考试时间：120分钟

二、试卷详细分析

三、试卷整体难度分析:中等

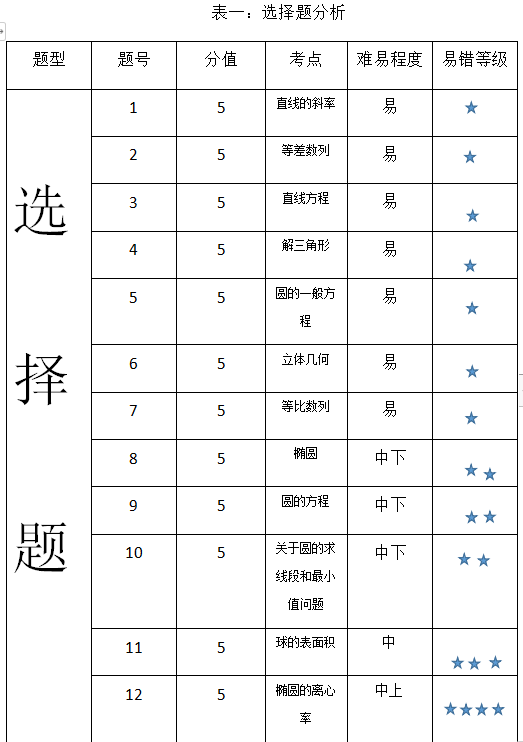
第一部分：选择题

该部分内容中：

第2、7题为上学期所学的内容，2题考察了等差数列求和公式，7题考查了等比数列的性质，难度很小。

第4题为上学期所学习解三角形这一章的内容，只需使用一个公式正弦定理。

第6、11题为本学期所学习的立体几何的内容，第六题难度较小可以使用余弦定理，也可选择做辅助线的方法。11题掌握如何找到外接球的半径，从而来求的球的表面积。

第8、12题为本学期所学内容，考查椭圆。椭圆这一章难度较大，计算量比较复杂。其中第8题椭圆结合向量一起考察，综合性较强，需要找到之间的关系。第12题求椭圆的离心率，结合平行四边形的性质，根据直线倾斜角的范围来确定椭圆离心率的范围。

第1、3、5、9、10题为本学期所学内容，考查直线与圆。1、3、5题难度较小，第9题可以数形结合，利用画图来解答思路更清晰，确定好所求圆的圆心和半径，最后写出圆的方程。第10题难度中等，求线段和最小问题，两动一定，做对称点，确定好Q和S点的位置。

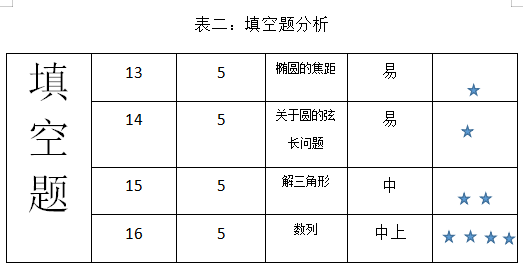
第二部分：填空题

第13题求椭圆的焦距，学生需要知道焦距等于2c，易错记为c。

第14题考查圆的弦长问题。

第15题为解三角形，考查了余弦定理和三角形面积公式和均值不等式，求边的最小值问题和通常想用均值不等式。

第16题为数列，这道题难度较大，首先我们需证明该数列为等比数列，写出其前n项和公式Sn，接着用分项求和求出Sn的前100项的和。

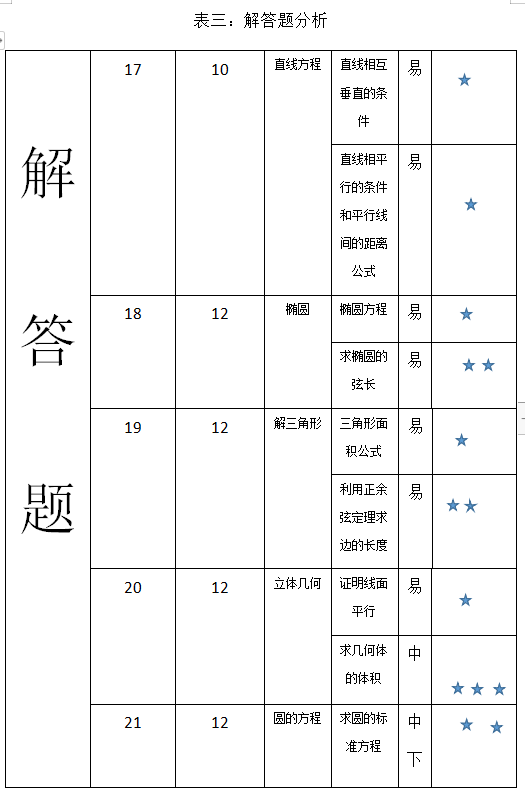
第三部分：解答题

第17题为直线的位置关系，考察直线平行和垂直的条件。当直线垂直时，斜率乘积为负1；当直线平行时，斜率相等。和平行线间的距离公式。

第18题为椭圆，第一问求椭圆方程，找到长轴长、焦距之间的关系即可。第二问考查了椭圆的弦长公式，这是椭圆的常考题型，难度不大，学生必须掌握弦长的求法。

第19题为解三角形，考查学生的转化能力。首先必须掌握正余弦定理和三角形面积公式。第一问只需用面积公式便可求出。第二问求边，主要考查学生正余弦定理运用的熟练度，本题难度较小。

第20题立体几何，第一问证明线面平行，证明平行我们用得最多的就是中位线，考查学生是否掌握了做辅助线的方法。第二问求几何体体积，掌握把一个不规矩的几何体拆分成若干个我们熟悉的几何体，最后利用体积公式求得。

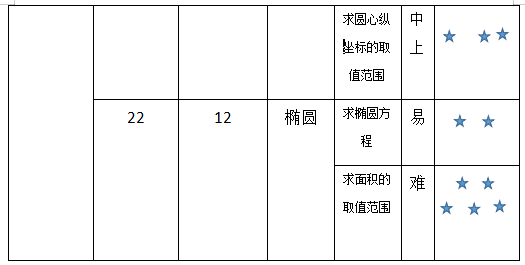
第21题为圆的综合习题，第一问首先根据题意设出圆的标准方程（尽量减少方程中的未知量），再根据弦长求出其圆的方程。第二问首先要明白题目考查的点在哪，先求出圆心的轨迹方程，该轨迹方程为圆，最后转化为两圆的位置关系（两个圆有交点R-r ~R+r）求出其圆心纵坐标的范围。

第22题为椭圆，是本章试卷的压轴题，难度较大，计算量复杂。第一问求椭圆方程，难度很小。本题的第二问将椭圆与圆结合，做圆的切线交椭圆于两个交点，还引入了向量，建议成绩在130以下的可以不做。

总结：

本次考试中，数列所占分值：15分，占比10%。解三角形所占分值：22分，占比14.7%。立体几何所占分值22分，占比14.7%。直线与圆所占分值：52分，占比34.7%。椭圆所占分值：39分，占比26%。

一中的月考试卷中，都会涉及到上学期所学的内容，所以建议同学们在考前一定要去复习。同时现在高二的难度也更大了，很多同学还没有适应，特别是椭圆这一章节，很多学生都不能做第一问，第二问多不清楚出发点在哪，所以我们应该掌握椭圆一些常考的题型，可以拿一些步骤分。高二上期主要是学习几何题，立体几何和解析几何，做题一定要数形结合，掌握做题的方法。

四、考后要求以及规划

1. 扎实的基础知识。基础知识好比地基，只有将地基无懈可击，方能有高楼的宏伟壮丽。

2. 注重培养学生的学习思维。数学是一个十分注重思维的学科，只有良好的思维，才能让抵抗变换多端的天气。

3. 注重对于题目解读，任何的题都需要题干支撑。只有对题干有着更好的解读，才能够将思维发挥。

4. 注意学生的课后学习习惯的引领。只有在良好的学习习惯之下，才会发现问题，思考问题，进而解决问题。

5. 对每一位学生的每一次作业的把控。需要认真分析，找出常错的地方，同时更需要帮助其改正。

6. 对于学生进阶的把控。则应当将每一个知识点进行分类，罗列出常考题型。并根据大数据，罗列出必考题型。进而对学生进行强化训练。